Territory may be of value to a nation for many reasons of strategy, sentiment, politics, or economics. We will assume that the reason of chief importance for the phenomena we wish to explore is economic. More specifically, we assume that the value to a nation of any territory is the increase in tax collections made possible by control of that territory, net of collection costs.
We further assume that there have been, in most places at most times, net diseconomies of scale in collection costs. This seems plausible, especially prior to the invention of such aids to bureaucracy as the printing press and the telegraph.
It follows from the foregoing that the size and shape of nations will be such as to maximize their joint potential net revenue and will approach from below the size which would maximize their potential gross revenue.[1]
Lastly, we assume that changes in the diseconomies of scale in the cost of collecting taxes are sufficiently small compared with changes in the economies of scale in amount collected that the latter largely determine changes in the size and shape of nations.
Before we try to apply this theory, several comments are in order. First, we make no assumption about how transfers of territory actually take place--whether the "loser" peacefully relinquishes his claim when it is clear he will be outspent or whether both nations must pay a price, in blood and treasure, to decide the issue. We merely assume that, in the long run, the territory ends in the possession of the nation willing to pay the higher price. Second, we do not assume that nations actually extract the highest possible taxes from their territories, new or old. It could be argued that, where they do not, it must be because they receive an even higher income in some other form from their restraint, but we will not explore that question.[2] We merely assume that having territory and taxing it to the limit is more attractive to a government than not having it at all and that a government is therefore willing, if necessary, to spend in acquiring territory up to the anticipated new revenues it could extract from the acquisition.
We will find it of interest to consider three different taxes and the effects they have on the size of nations--taxes on land, taxes on trade, and taxes on labor. In classifying taxes, we are concerned not with the form of the tax but with what factor actually ends up paying it; a tax on the export of grain, for example, may in fact be paid by a reduction in rents on land.
Since our argument forces us to consider potential taxes, the existence of actual taxes is of interest only as proof that those particular taxes could be collected. The absence of other taxes may suggest that they could not be collected, but potential taxes are defined not by what was collected but by what resources were available to be seized by the state and at what cost. The terms "nation" and "state" are imprecise, especially when applied to a variety of historical periods. Since our theory will rest on the economies of tax collection that result from coordination, we define a t-nation as the largest political unit within which tax policy is effectively coordinated. A feudal kingdom some of whose feudatories independently set tolls across their domains would be composed of several t-nations. A weak nation whose tax policies were dictated by a powerful neighbor would not be a t-nation, nor would any one of several nations that coordinated tax policies for mutual benefit. A Zollverein is a single t-nation with respect to customs, but its members may be separate t-nations with regard to other taxes.
This last example brings out an ambiguity in our definition. What is or is not a t-nation sometimes depends on the particular tax considered. There is a further ambiguity in the phrase "effectively coordinating" which we will for the moment ignore.
For the collection of taxes on trade, there exist economies of scale (in revenue, not in collection costs) up to the length of a single trade route or the width of a network of parallel trade routes. The reason is that several t-nations along a single trade route, each setting its tax rates to maximize its own income, will have a combined rate above their joint optimum. Similarly, several t-nations sitting on parallel trade routes (routes running between the same two points by different paths) will have tax rates below their joint optimum. In either case, total revenues could be increased by combining several t-nations into one.
For the collection of taxes on land, there seem to be no similar effects. A state, whatever its size, can tax up to the full economic rent of land and no more.[3] Taxes on labor present a more complicated picture but one in some ways similar to the case of parallel trade routes. In that case, each nation has an incentive to undertax, in order to increase the trade along its route at the expense of its neighbors. Similarly, where several nations tax a mobile labor force, each is limited in its tax rates by the fear of losing population to the others.[4] One way to raise the cost of emigration is to make a nation larger. Another is to restrict mobility forcibly--to chain the serf to the land[5] or line the border with barbed wire. Since the ratio of border to area declines with increasing size, this again gives an efficiency advantage to larger nations.
Another strategy, and one which avoids the administrative diseconomies of larger nations, is to shape national boundaries in such a way as to make emigration prohibitively expensive. If all the places you want to live--all the places where people speak your language and share your culture--are in one t-nation, emigration, even to escape high taxes, may seem unattractive. "
Some Preliminary Tests of the Theory
To test our theory, we must identify t-nations; that might best be done by carefully examining the political and diplomatic history of every nation in the area we are considering, in order to determine which were single t-nations, which were made up of several t-nations, and which were component parts of larger t-nations. Such a study would be beyond the scope of this paper. Instead, I used the following rules:
1. Anything identified as a state in the standard historical atlases[13] was assumed to be a t-nation except for the Holy Roman Empire after 911 and France from 987 until 1400. In these two cases, the component states or major feudatories were considered t-nations for taxes on trade.[14] Zollvereinen were also considered t-nations for taxes on trade.
2. Where more than one state was under a single ruler, the group of states was considered a single t-nation (this includes states under the church).
A second problem is the paucity of economic and demographic data for the periods we wish to study. This was dealt with by a variety of simplifying assumptions which will be described.
Given the difficulties of testing our theory and the limited scope of this paper, I prefer to regard this section as a preliminary set of tests, designed more to show how the theory might be tested than to confirm or refute it conclusively.
Taxes on Trade
If our arguments are correct, t-nations should tend to shape themselves so as to maximize the total revenues received from taxes on trade, and that tendency should be greater as the amount of trade available to be taxed is greater. We do not expect to observe a perfectly efficient outcome, partly because our information with respect to both trade routes and political boundaries (of t-nations) is imperfect but also, more importantly, because shaping nations to maximize tax revenue from trade is costly. We do expect that the larger the amount of trade, the higher the cost a nation is willing to bear in order to tax it more efficiently and so, ceteris paribus, the higher the tax-efficiency index (TEI). Whether the relevant variable is the absolute value of trade or its value relative to other sources of revenue is somewhat unclear in our model. To the extent that the costs of shaping a t-nation to tax trade efficiently are independent of its total revenue and of that of other t-nations, it is the absolute value of trade which is relevant; to the extent that the costs are proportional to total revenues (either because they involve administrative costs which increase with increasing volume of government or because they involve the costs of conflicts with neighboring states), it is the relative value of trade in relation to the value of other revenue sources.
To construct an index of tax efficiency, I assumed that trade declines linearly with total taxes on the trade route. Let the total volume of trade along a single trade route be V, the number of nations taxing the route be n, the tax rate of the ith nation be TI , and the total tax rate along the route T. We have
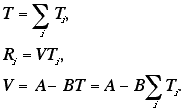
By definition, t-nations maximize independently. So nation i sets TI to maximize its revenue, RI:
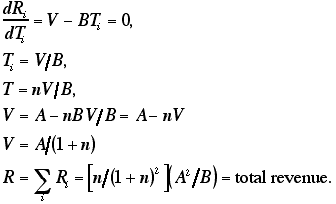
So we see that, where n nations control a single trade route, the total revenue collected will be proportional to n/(n + i)2. When two nations each control one of two parallel trade routes between the same two points, the assumption of independence implies that they will collect no taxes at all; as in the familiar case of perfect competition, all profits are competed away. We compute our TEI, for a given political map and a given set of trade routes (see figs. 1 and 2), by calculating the total tax collected under these assumptions and dividing it by the total tax that would have been collected had each trade route been controlled by a single t-nation.
Consider, for example, the trade route labeled i on figure 1A, which follows the Adige River from Trent to the Adriatic. It goes through the territory of two nations, as shown by its diagram on figure 2A. So n is 2, the total tax revenue that would be collected is (2/9)(A2/B), the total tax collected by a single revenue-maximizing state controlling the same route would be (1/4) (A2/B), so the TEI for that particular route is 8/9.
Now consider route ii on figure 1A, running along the Po from Pavia to the Adriatic. Here, as in all our calculations, we assume that a nation must control both banks of a river at one point in order to control commerce passing along the river at that point. Since for most of the route the two banks of the river are controlled by different nations, one has in effect two parallel routes, one controlled by Lombardy-Venetia and one by Sardinia and then by Parma. The routes join into one where the river flows through Lombard-Venetian territory, then separate again where it becomes the border between Lombardy-Venetia and the Papal States. Finally it flows again through Lombard-Venetian territory to the Adriatic. The situation is diagrammed in figure 2A. Since parallel routes under our assumptions produce no revenue, we may remove the parallel segments, yielding diagram ii' of figure 2A. We see that, in spite of the complication of the original diagram, only one nation (Lombardy- Venetia) is in a position to tax the trade route. No boat without permission from the Lombard-Venetian authorities may travel from Pavia to the sea; any boat having such permission may, without permission from any other nation, simply by keeping to the left bank of the Po. So n is 1, and the TEI for this route is unity. The TEIs calculated from figures 2A and 2B are shown in table 1.
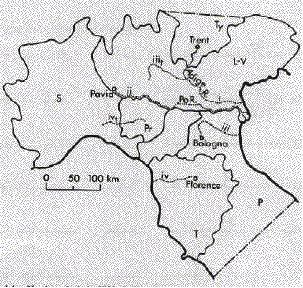
S: Kingdom of Sardinia; LV: Lombardy-Venetia; Ty: Tyrol; Pr: Parma; P: Papal States; T: Tuscany.
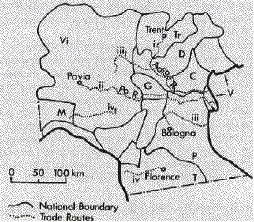
Fig. 1B.--Northern Italy in 1378. Vi: domains of the Visconti; M: Marquisate of Montferrat; C: Gonzaga; Tr: Bishopric of Trent; D : Della Scala dominions; C: Carrara; V: Venetian Republic; P: Papal States; T: Tuscany. (Tr and P are parts of the same t-nation.)
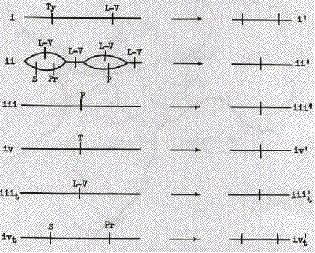Fig. 2A.--Schematic diagrams of trade routes, northern
Italy, 1854
To construct our trade routes, we utilized the fact that water transport was until the nineteenth century very much cheaper than land transport.[15] Our first set of trade routes was constructed by finding, on an economic map of Europe in 1500 (Putzger 1965, pp. 70-71), all cities of over 20,000 people and connecting them to the sea by any available navigable rivers.[16] Routes iii and iv on figures 1A and 1B are examples. All routes were assumed to have the same amount of trade, save that those from cities of over 50,000 were treated as having twice the trade of the others. The TEI was calculated for each city's trade routes and the results averaged, with the large cities being counted twice. The efficiency indices calculated from these trade routes are shown in the first row of table 2.
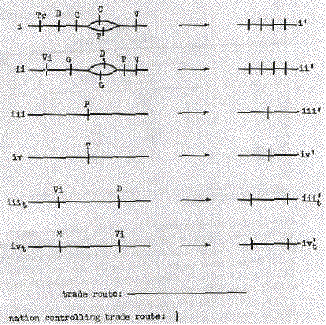Fig. 2B--Schematic diagrams of trade routes, northern
Italy, 1378
It may be objected that, by using a single set of trade routes for all times, we ignore the possibility that economic change may have altered the pattern of trade. But if we recalculate the trade routes at each period, we run the risk that a high or rising TEI may reflect trade routes adapting themselves to the shape of nations rather than the other way around. By calculating trade routes on the basis of early data, we at least guarantee that, if the TEI rises after the medieval period, as we expect, it will do so in spite of, not because of, the imperfections of our method.
The larger nations are, the fewer of them a trade route will on average go through. So a high TEI might be merely a side effect of some other factor that made nations large. To eliminate such effects and determine to what extent t-nations actually shaped themselves to trade routes, I constructed a second set of "trade routes" very similar to the first, save that there was no reason to expect any trade on them. They were constructed by translating each real trade route by 100 kilometers in each of two orthogonal directions.[17] Routes iiit and ivt on figures 1A and 1B are the routes corresponding to iii and iv. These imaginary trade routes provided the control; I calculated the tax-efficiency index for them just as for the real trade routes. I then divided the real TEI by the control TEI, to give a measure of the degree to which nations shaped themselves to trade routes. The results are shown in line 2 of table 2.
| TABLE 1 | ||||||
|---|---|---|---|---|---|---|
| Route |  |
|
||||
| i | ||||||
| ii | ||||||
| iii | ||||||
| iv | ||||||
| iiit | ||||||
| ivt | ||||||
 |
||||||
 |
||||||
* Corresponds to line 2, table 2.
+Corresponds to line 4, table 2.
One defect in this procedure is that our real trade routes are rivers, and our controls are not. Rivers may affect the shape of nations in ways unrelated to our theory (in particular by providing easily defended boundaries), and such effects may distort the results shown on line 2 of table 2.
To avoid this problem, I constructed another set of trade routes and controls. I used the economic map to estimate the relative amount of trade on different rivers. I then selected a group of the highest-trade rivers and paired each with a nearby low-trade river of comparable length; the first set I used as my trade routes, the second as my controls.[18] Route ii on figures 1A and 1B is a high-trade river and route i the corresponding low-trade river. The results are shown on lines 3 and 4 of table 2.
| TABLE 2 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
1. Cities
|
||||||||||||||
2. Cities/cities displaced
|
||||||||||||||
3. High-trade rivers
|
||||||||||||||
4. High trade/low trade
|
||||||||||||||
The results of these calculations are somewhat mixed. The absolute TEIs behave about as we would expect, reaching their lowest value from about 1,000 to 1,400 and then rising. The relative TEIs are less satisfactory. The values shown in line 2 of table 2 seem to fluctuate almost randomly; those shown in line 4 rise, as one would expect, with increasing trade in the sixteenth, seventeenth, and eighteenth centuries but show no previous dip. Both lines show dips in the second half of the nineteenth century and in the twentieth. One explanation is that, as nations became large, the tax efficiency became high even for a random set of trade routes; a one-nation world, after all, is perfectly tax efficient for any set of routes. Another explanation is that our trade routes were calculated from an economic map for 1500, using an assumption (water transport) designed for a premodern world. The later the date, the less likely it is that our "trade routes" actually carry more trade than our "controls." A third explanation is that the dip reflects the declining relative importance of taxes on trade.
The Effect of Taxes on Labor
According to our arguments, nations should tend to shape themselves so as to include entire linguistic groups within their borders, and the degree to which they do so should be greater as the amount of their revenue derived from taxes on labor is greater. The argument does not necessarily imply that nations will tend toward linguistic homogeneity; a nation containing all of two language groups is not more subject to tax competition than a nation containing all of one (although it may be unnecessarily bearing other diseconomies related to its size). It does imply that linguistic regions will tend to become nationally homogeneous, that one linguistic region will tend to consist only of territory belonging to a single t-nation. To test this conjecture, we calculate the linguistic homogeneity index (LHI), defined as the average over all persons of the percentage of speakers of each person's language who live in the same t-nation as he does. Formally
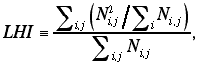
Where Nij is the number of people in nation i speaking language j. This index, unlike TEI, is not derived from any actual calculation of taxes that will be collected, since we do not have a satisfactory simple model of this kind of tax competition.[19] We expect, however, that the larger the percentage of a citizen's language group living outside his nation, the easier it is for him to migrate and the lower, in consequence, the taxes that can be collected from him.
In order to evaluate the index, one requires a census of the number of speakers of each language in each i-nation. For many of the times at which we wish to evaluate it, no such data exist. I have therefore made several simplifying assumptions. The first is that the linguistic map of nineteenth-century Europe accurately represents linguistic boundaries from the twelfth century to the present. This assumption appears plausible, to judge by the near identity among linguistic maps of central Europe in 1500 and Europe in the nineteenth and twentieth centuries.[20] The second assumption is that the relative populations of linguistic regions have stayed the same over the same period.[21] The third is that the population of each linguistic region at every time is uniformly distributed over the region. It would be possible, but laborious, to improve on these assumptions by the use of such historical data on population as are available.
Of the unrealistic elements in our assumptions, only one seems likely to effect qualitative results. Our linguistic map differentiates only crudely among dialects.[22] At the earliest times we are considering, variations among dialects were many and large; even today the difference between, say, Austrian and Swiss German (both of which are here classified as High German) is substantial. I may have underestimated the LHI for the earliest periods by ignoring differences between dialects that were at that time virtually separate languages. Using these assumptions, I calculated values for LHI. They are shown on line 1 of table 3 and in figure 3.
Here, as with taxes on trade, we would like to separate out the effects of changes in the size of nations from changes in their shapes. To do this, we select matched groups of countries at adjacent dates, by the following procedure.
First, for each pair of adjacent dates (1250 and 1360, e.g.), we calculate the combined population (measured as a fraction of the combined population of all nations)[23] of the 15 largest nations (by population).
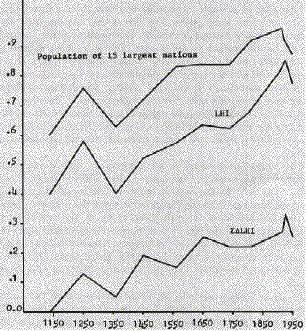Fig. 3
This is shown on line 2 of table 3 and graphed as line 2 of figure 3. Since the figure for 1250 is larger than for 1360, we proceed to choose a group of 15 nations in 1250 whose combined population is the same as that of the 15 largest nations in 1360. Our choice rule is to order the nations by size, remove a consecutive sequence of n nations, calculate the combined population of the 15 largest nations remaining, and compare it with the population we are trying to match. We start with n = 0 and continue until we have a match to within 2 percent; if the same value of n generates two different groups that match to within 2 percent, we take the closer match.
Having chosen our groups of 15 nations (the 15 largest in 1360 and a matching group of 15 in 1250), we calculate the LHI for each group. Their difference is shown as
LHI on line 3 of table 3. It is a measure of
the change in LHI from one date to the next caused by changes in the shapes of
nations, independent of changes in their sizes. The sum of LHIs from 1140 on is
shown on line 4 of table 3 and graphed in figure 3; it represents the cumulative
change in linguistic homogeneity controlling for changes in nation
size.| TABLE 3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
1. LHI
|
|||||||||||
2. Population of 15 largest
nations*
|
|||||||||||
3.
LHI
|
|||||||||||
4.
 LHI |
|||||||||||
*as a fraction of total for all countries.
The results of our calculations appear to fit reasonably well our expectation that the LHI should increase whenever income, as a potential source of tax revenue, increases relative to trade and rent. The upper two curves of figure 3 have two sections of sustained growth; one follows the Great Plague, the other parallels the Industrial Revolution. The lower curve has its largest single rise in the century after the plague and rises also through the nineteenth and early twentieth centuries, but the rest of the pattern is less clear. All three curves decline sharply during the last period (1922-50). While our theory can explain this decline as the result of a shift from one method of preventing exit to another, it does not predict it.
According to our theory, a high LHI reflects one way in which a nation prevents its taxpayers from emigrating. Nations which prohibit exit by force should have less incentive to take advantage of linguistic barriers; a Hungarian who is prepared to crawl across barbed wire into Austria is not likely to be deterred by the need to learn a new language once he arrives. So iron curtain countries should tend to have a lower LHI than other similar countries. To test this conjecture, I calculated the LHI for the iron curtain countries in 1950 and for a group of non-iron curtain countries containing the same number of countries and the same total population. The iron curtain countries, as shown in table 4, had a lower value of the index. In order to check whether this reflected anything more than differences in the linguistic distributions of eastern and western Europe, I made a similar calculation for the same areas in 1922. The western countries still had a higher value of the index, but the difference was less than half as great. While I would not like to claim very much significance for the results, it is at least encouraging that they fit our theory.
I would say much the same about the results of all the tests described in this paper. Although some specific features do not fit our expectations, the results tend on the whole more to confirm than to contradict our theory. I will be happy if they convince those better qualified in economic and political history not that our theory is true but that it is worth the effort required to test it further.
| Table 4 | |||||
|---|---|---|---|---|---|
1950 Iron curtain |
1950 Non-Iron Curtain* |
1922 "Iron Curtain"** |
1922 "Non-Iron Curtain * *** | ||
| 1 | 2 | ||||
| LHI | .81 | .88 | .78 | .81 | .81 |
| Population§ | .38 | .38 | .32 | .32 | .32 |
*A selection containing same number of countries and same total population as the iron curtain countries. http://www.daviddfriedman.com/Academic/Size_of_Nations/Size_of_Nations.html
