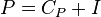Market Earth: toy thinking : considering the equation below...does the volume of investment determine profits or vica versa ?

Sunday, April 29, 2012

toy thinking : considering the equation below...does the volume of investment determine profits or vica versa ?

$\textstyle P=C_P+I$ ,

in a simple model this holds of income is either profits or wages and each class is distinct
and if wages every period are always spent in full the next period

P(t) => C( t + 1) + I( t +1)

C (t) + I (t)=> P (t+1)

“The answer to this question depends on which of these items is directly subject to the decisions of capitalists. "

"Now, it is clear that capitalists may decide to consume and to invest more in a given period than in the preceding one, but they cannot decide to earn more."
yes they can spended their income or les then their income

" therefore, their investment and consumption decisions which determine profits, and not vice versa”.^[

^{voila sez M Kalecki}

if so consider C (T)
( capitalist class spending on household products)

lets hold C constant from t to t+1

then P in (t +1 ) is a function of I(t)
next period profits are a function of this period I

generalize some

let C vary over T
using
a fixed part A
and some fraction q of P
ie
$\textstyle C_P=A+q \cdot P\,\$

BRING back in I
if
I = P -(A +q.P)
then
P = I + (A + q.P)
or
in a steady state path:

$\textstyle P= \frac{A+I}{1-q} \,\$ ***

^{okay can we use this to claim to push for higher effective demand along the following lines ?}
^{can we force up investment ? in a liquidy trap no}

^{so enter public spending G and is offset taxes on profits T}
^{forget the taxes on wages hey say they don't exist}
^{all taxes are on profits}

^{if G-T this period t is larger then last period P(t-1) - ( I (t) + C(t) )}
^{then this period P will be larger then if G-T equals zero}

^or
^{why would corporate elites now prefer stagnation in the oecd}

^{*** P=I + A +q.P}

^{P - q.P =I + A}

^{P(1-q) = A+I}

^{P=A +I/1- q}